World Wide GEB

GEB
Дуглас Р. Хофштадтер.
[ предыдущая ] [ оглавление ]

Перевод Александра Семенова

Г Л А В А IV
Непротиворечивость, Полнота и Геометрия

Явный и скрытый смысл

Во второй главе мы видели как смысл (по крайней мере, в относительно простом контексте формальной системы) возникает если установлен изоморфизм между символами, которыми манипулируют по правилам, и объектами реального мира. Чем более сложен этот изоморфизм в целом, тем больше нужно "затратить" усилий и средств, для извлечения смысла из символов. Если изоморфизм очень прост (или знаком) мы склонны говорить, что смысл, который мы видим, - явный. Мы видим смысл, не замечая изоморфизма. Наиболее яркий пример этого - человеческий язык, где люди часто приписывают смысл словам в себе, вместо того чтобы найти в самом незначительном отзвуке очень сложный "изоморфизм", который и наполняет их смыслом. Это ошибка, которую легко сделать. Люди скорее приписывают признак объектам (словам их обозначающим) чем связям между этим объектами и реальным миром. Это можно сравнить с наивной верой, что шум - необходимый эффект от столкновения двух объектов. Но это- заблуждение. Если два объекта сталкиваются в вакууме, то никакого шума вообще не возникнет. Ошибка возникает оттого, что шум приписывают столкновению, но они теряют из внимания роль среды, которая переносит энергию от объектов к уху.

Выше я использовал термин "изоморфизм" в кавычках, указывая этим, что оно должно приниматься с некоторой натяжкой. Утонченный процесс, который лежит в основе процесса восприятия и понимания человеческого языка гораздо сложней, чем операции над символами в типичных формальных системах. Мы должны будем принять (если мы хотим и далее думать о смысле как о проявлении изоморфизма) гораздо более гибкую идею. Придется признать, что изоморфизмы могут быть более широко привлечены для объяснения процесса понимания, чем было принято. По моему мнению, фактически, ключевым элементом в ответе на вопрос "Что такое сознание?" будет проникновение в сущность "изоморфизма", который лежит в основе того, что мы называем смыслом.

Явный смысл Контракростихпункта

Все это только подготовка к обсуждению различных уровней смысла, которыми наполнен Контракростихпунк. Диалог имеет и явное и скрытое содержание. Наиболее явный уровень смысла в том, что здесь просто рассказана некоторая история. Этот "явный" смысл чрезвычайно неявен в том значении, что мыслительные процессы, вовлеченные в понимание событий истории (запечатленных только в виде сплетения черных черточек на бумаге) невероятно сложны. Однако мы рассмотрим происходящее в Диалоге в самом явном значении и предполагаем, что всякий читающий на человеческом языке использует более-менее похожий "изоморфизм" и в результате извлечет более-менее похожий смысл из символов на бумагу.

Но даже в таком случае я хотел бы быть несколько более четким относительно явного смысла данной истории. Сначала я буду говорить по поводу проигрывателей и пластинок к нему. Здесь главный момент в том, что имеется два уровня осмысления роли звуковых дорожек пластинки. Уровень I - это музыка. Но "Музыка", это последовательность колебаний частиц воздуха или последовательность эмоциональных реакций в мозге? И то, и то. Но прежде чем возникнут эмоциональные реакции, должны присутствовать колебания воздуха. Далее, колебания воздуха генерируются из звуковых дорожек проигрывателем. Проигрыватель - относительно простое устройство. Фактически, вы можете получить звук напрямую, только проведя булавкой вдоль дорожек звукозаписи. После этой стадии ухо преобразовывает звуковые колебания в импульсы слуховых нейронов мозга. Далее происходит множество этапов преобразований в коре мозга, которые постепенно превращают звуковые колебания в сложное сплетение эмоциональных реакций. Этот процесс слишком сложен для нас, чтобы, начав в нем разбираться здесь, к концу книги сколько-нибудь преуспеть. Поэтому, позвольте мне удовлетвориться рассуждениями об "Первом Уровне" содержания звуковых дорожек как о звуке в воздухе. Каков же смысл Уровня Два для тех же дорожек? Это резонансные колебания, возбужденные в проигрывателе. Это содержание может проявить себя только после проявления Уровня Один, который сам возникает непосредственно из дорожек, так как колебания проигрывателя вызываются только колебаниями воздуха. Получается что Второй Уровень смысла зависит от цепи двух изоморфизмов:

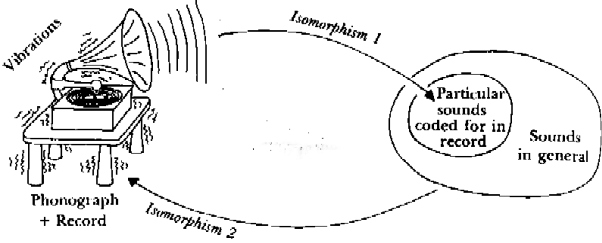
РИС. 20. Схематическое представление принципа, лежащего в основе Теоремы Геделя: два отображения "один в другой", которые имеют неожиданный эффект бумеранга. Первое отображает форму дорожек звукозаписи на звуки, производимые фонографом. И тут же (знакомое, но обычно игнорируемое явление) звуки вызывают колебания фонографа. Обратите внимание, что второе отображение существует независимо от первого. Звук из любого источника (не только произведенного фонографом непосредственно) причинит подобные колебания. Перефразируя Теорему Геделя скажем, что для любого проигрывателя, имеются записи, которые на нем нельзя сыграть, потому, что они приводят его к косвенному саморазрушение. [Рисунок автора]

Эта цепь изоморфизмов показана на рис. 20. Заметьте, что изоморфизм 1 - тот, который соответствует Первому Уровню содержания дорожек. Второй Уровень содержания грамзаписи является менее явным, чем Первый, потому что он проявляется только в цепи двух изоморфизмов. Этот второй уровень содержания, который и вызывает "неприятные последствия" - гибель проигрывателя. Что интересно, извлекая Первый Уровень, мы одновременно извлекаем Второй. И нет никакого способа извлечь Первый без Второго. Так что, Второй был изначально неявным содержание грамзаписи, которое обернулось против нее же, разрушив пластинку.

Подобный комментарий применим и к кубку. Одно отличие - переход от букв алфавита к нотным знакам- это еще одни уровень изоморфизма, который мы можем назвать "транскрипция". Выбранный термин следует из его перевода - преобразование музыкальных нот в музыкальный звук. Далее звук, то есть колебания воздуха, воздействует обратно на кубок точно также, как он воздействует на любой образец из предложенных проигрывателей.

Скрытый смысл Контракростихпункта

Что по поводу скрытых смыслов Диалога? (Их действительно несколько). Самый простой из них, был уже упомянут. А именно то, что события в двух частях Диалога приблизительно изоморфны друг к другу. Фонограф становиться скрипкой, Черепаха становиться Ахиллесом, Краб становиться Черепахой. Дорожки звукозаписи становятся автографом, гравированным на кубке и т.д. Как только вы обнаруживаете этот простой изоморфизм, вы можете продвинуться дальше. Следите: в первой половине Черепаха источник всех зол, в то время как во второй половине он - жертва. Как вы знаете, его собственный метод, обращается против него же неприятными последствиями! Напоминает ли это о неприятностях возникших из музыки его пластинок, или надписи на кубке? Или это напоминает о прекрасной коллекции бумерангов, собранных Черепахой?
Да, действительно, история с неприятными последствиями происходит на двух уровнях...

Уровень Один. Кубок и грамзаписи, которые приводят к неприятным последствиям.

Уровень Два. Дьявольский метод Черепахи (использовать скрытое содержание, чтобы вызывать неприятные последствия) вызывает неприятные последствия.

Поэтому вы даже можете видеть изоморфизм между двумя уровнями истории. Мы приравниваем способ, каким грамзаписи и кубки бумерангом бьют сами по себе со способом, какими жесткие методы Черепахи бумерангом бьют по нему самому. Обратите на это внимание.

Взаимное отображение между Контракростихпунктом и Теоремой Геделя

Возможно, вас это уже слегка укачало - но лучшее впереди. (По сути, некоторые уровни скрытого смысла мы здесь даже не будем обсуждать, они оставлены для вас, как загадка) Самой глубокой причиной для написания этого Диалога было стремление иллюстрировать Теорему Геделя, которая, как я сказал в предисловии, опирается на два различных уровня смысла утверждений теории чисел. Каждая из половинок контракростихпункта - "изоморфная копия" Теоремы Геделя. Поскольку это отображение - центральная идея Диалога и она довольно сложное, я тщательно прорисую его ниже:

Проигрыватель <==> аксиоматическая система для теории чисел
Проигрыватель низкого качества <==> "слабая" аксиоматическая система
Высококачественный проигрыватель <==> "сильная" аксиоматическая система
"Совершенный" проигрыватель <==> полная аксиоматика теории чисел
"Проект" фонографа <==> аксиомы и правила формальной системы
Грамзаписи <==> цепочки формальной системы
Проигрываемые записи <==> теорема аксиоматической системы
Не проигрываемые записи <==> не теоремы аксиоматической системы
Звук <==> истинные утверждения теории чисел
Воспроизводимый звук <==> интерпретируемая теорема системы
Не воспроизводимый звук <==> истинное утверждение, не являющееся теоремой
Название песни: <==> скрытый смысл выражения Геделя:

"Я Не могу Быть Сыгран "Я не могу Быть Получен
На проигрывателе X " в Формальной Системе X "

Это не полное описание изоморфизма между Теоремой Геделя и Контракростихпунктом, но это - ядро, самое главное. Не стоит волноваться по поводу того, полностью ли вы ухватили смысл Теоремы Геделя к настоящему моменту. Впереди все еще имеется несколько глав, которые следует преодолеть, прежде чем мы достигнем цели. Однако, читая этот Диалог, вы уловили дух теоремы Геделя без необходимости досконального знания ее. Теперь я оставлю вас с этим, что бы разыскать другие скрытые смыслы в Контракростихпункте. "Quaerendo invenietis!"

Искусство фуги

Несколько слов об Искусстве фуги... Созданное в последний год жизни Баха, оно представляет собой основанное на одной теме собрание восемнадцати фуг. Очевидно, написание Музыкального Приношения служило источником вдохновения Баху. Он решил написать новое собрание фуг, которые были бы основаны на одной очень простой теме. Варьируя ее, он хотел продемонстрировать широкие возможности, присущие форме. В Искусстве фуги Бах использует одну единственную тему, но самыми разными виртуозными способами. Вся работы выполнена в едином ключе. Большинство фуг имеют четыре голоса, и они постепенно увеличиваются в сложности и глубине выражения. В конце они поднимаются к таким утонченным высотам, что, кажется, нет никакой больше возможности развивать сложность музыки дальше. И все же он это делает . . . до последнего.

Контрапункт

Обстоятельства, которые прервали написание Искусства фуги (здесь надо вспомнить обстоятельства жизни Баха) заключалось в его зрении, беспокоившем его на протяжении многих лет. Бах хотел сделать операцию. Это было сделано, однако результаты оказались очень плохими, и как последствия он потерял зрение вообще на последней части года своей жизни. Однако это не остановило его энергичной работы над монументальным творением. Его цель - представить полный спектр возможных вариантов фуг и многократное использование для этого одной темы было важным фактором. В том, что он планировал как предпоследняя фуга, он вставил свое собственное имя, закодированное в нотах как третья тема. Однако к этому моменту времени его состояние здоровья стало настолько сомнительным, что он вынужден был отказаться от работы над взлелеянным проектом. В начале болезни он сумел продиктовать зятю заключительную часть хорала, о которой биограф Баха Фокель (Forkel) написал: "Выражение покорного смирения и набожности всегда охватывают меня, когда я играл это. Так что я еда смогу сказать, что бы предпочел потерять - этот Хор, или конец последней фуги."

В один день, внезапно к Баху вернулось зрение. Но несколькими часами позже он перенес удар и спустя десять дней умер, оставив другим размышлять о неполноте Искусства фуги. Интересно, можно ли поэтому сказать, что здесь Бах достиг самоссылки?

Проблемы, вызванные результатами Геделя

Черепаха утверждает, что недостаточно мощный проигрыватель может быть совершенен в том смысле, что он может воспроизводить каждый возможный звук грамзаписи. Гедель говорит, что недостаточно мощная формальная система может быть совершенна, в смысле воспроизведения каждого отдельного истинного утверждения как теоремы. Но так же как Черепаха утверждает о проигрывателе, этот факт только похож на дефект, если вы имеете нереалистичные ожидания относительно того, что формальная система должна делать. Однако математики вступили в это столетие (XX -А. С.) именно с такими нереалистичными ожиданиями. Полагая, что аксиоматические рассуждения окажутся панацеей от всех бед. Они выяснили обратное, только в 1931 году. Факт, что истина не вмещается в "пространств" теорем любой данной формальной системе, называется "неполнотой" системы.

Наиболее озадачивающий факт, относительно методов доказательства Геделя, то, что он использует методы рассуждений, которые, по всей видимости, не могут быть "инкапсулированы" - они сопротивляются включению в любую формальную систему. Таким образом, на первый взгляд, кажется, что Гедель раскопал до настоящего времени неизвестное, но глубоко существенное различие между человеческими рассуждениями и рассуждениями механическими. Это мистическое различие в мощности между живыми и неживыми системами отображается в несоответствии между понятием истины и пространства теорем. . . или, по крайней мере, является "романтическим" способом смотреть на ситуацию.

Измененная pq-система и противоречивость

Чтобы увидеть ситуацию более реалистично, нужно гораздо глубже видеть, почему и как смысл в аксиоматических системах образуется изоморфными связями. И я полагаю, что это ведет еще к более романтическому взгляду на ситуацию. Поэтому теперь мы продолжим рассматривать некоторые другие аспекты отношений между смыслом и формой. И наш первый шаг - мы должны сделать новую формальную систему, слегка изменив старого друга, pq-систему. Мы добавим еще одну схему аксиом (сохранив первоначальную схему, так же как и единственное правило вывода):

Схема аксиом II: Если х - цепочка дефисов то xp_qx аксиома.

Ясно, что тогда _ _ p _ q _ _ - является теоремой в новой системе (все аксиомы -теоремы) и так же _ _p _ _ q _ _ _. И все же их интерпретация соответственно, "2 плюс 1 равно 2", и "2 плюс 2 равно 3". Но легко заметить, что наша новая система будет содержать много ложных утверждений (если вы будете рассматривать цепочки как утверждения). Таким образом, наша новая система непоследовательна или противоречива с внешним миром.
Как будто этого было мало, но мы так же имеем внутренние проблемы с нашей новой системой, так как она содержит утверждения, которые не согласуются друг с другом, типа
_ p _ q _ _ (старая аксиома) и _ р _ q _ (новая аксиома). Так что наша система противоречива во втором смысле - внутренне.
Было бы, поэтому, единственно разумным решением - выбросить эту систему? Вряд ли. Я специально представил эти "противоречия", чтобы поводить вас за нос. Я пробовал выразить нечетко-представимые аргументы настолько аргументировано, насколько это возможно, чтобы ввести вас в заблуждение. Возможно, вы легко уловили подвох в том, что я тут изложил. Критическая ошибка произошла тогда, когда я без сомнений принял те же самые интерпретирующие слова для новой системы, что и для старой. Помните, имелся только один повод для того, чтобы использовать для интерпретации те слов, в прошлой главе, и причина была в том, что символы действовали изоморфно к идеям, они были согласованы с интерпретацией. Но когда вы изменяете правила, которые управляют системой, вы неизбежно разрушите изоморфизм. И этому ничем нельзя помочь. Поэтому все проблемы, которые притворно оплакивались в предыдущих абзацах, оказались поддельными. Они могут обратиться в ничто, если вы соответственно дадите иное толкование некоторым символам системы. Заметьте, я сказал "некоторым". Не обязательно чтобы все символы отображались именно на новые понятия. Некоторые могут сохранять свои старые "значения", в то время как другие изменяться.

Непротиворечивость восстановлена

Давайте, например, предположим, что мы по-другому интерпретируем символ q, оставив все остальные интерпретации - теми же. В частности, интерпретируем q фразой "больше или равно". Теперь наши "противоречащие" теоремы _ p _ q _ и _ p _ q _ _ получаться вполне совместимыми: "1 плюс 1 больше или равно 1" и "1 плюс 1 больше или равно 2". Мы одновременно избавились (1) от противоречия с внешним миром и (2) от внутренних противоречий. Наша новая интерпретация - осмысленная интерпретация, в то время как первоначальная, несомненно, бессмысленна. То есть она бессмысленна в нашей новой системе, а для первоначальной pq-системы она подходит по-прежнему прекрасно. Но первоначальная интерпретация кажется бессмысленной и нелепой, если применить ее к новой, pq-систем. Она здесь настолько же уместна, как "яблочно-лошадино-счастливуая" интерпретация уместна к старой pq-системе.

История Евклидовой геометрии

Хотя я и пытался застать вас врасплох и немного удивить, но этот урок о интерпретации символов словами, не кажется слишком трудным как только вы видите суть предмета. Но на практике это не всегда так. В этом состоял один из самых глубоких уроков математики девятнадцатого столетия! Все началось с Евклида, который около 300 года до нашей эры систематизировал и интерпретировал все, что было известно относительно планиметрии и стереометрии в его дни.
Окончательный труд, Начал Евклида, были настолько строен и прочен, что стали фактически библией геометрии в течении более чем двух тысяч лет. Начала - наиболее непоколебимый труд всех времен. Почему?
Основная причина в том, что Евклид был законодателем строгости в математике. Начала начинаются с очень простых идей, определений и т.д. Все это постепенно вырастает в обширное здание результатов, организованных таким способом, что любой конкретный результат зависел только от предшествующих результатов. Таким образом, имелся определенный план работы, структура которого сделала всю громаду геометрии стройным и прочным сооружением.
Однако архитектура этой конструкции была отличной от, например, привычной нам архитектуры небоскреба (см. рис.21) В последнем случае, если здание стоит, то это доказывает, что все его структурные элементы держат его нагрузку. Но в книге по геометрии, когда каждое суждение требует, чтобы оно логически следовало из более ранних суждений, не будет никакого крушения, если одно из доказательств недействительно. Здесь балки и распорки не физические, а абстрактные объекты. Фактически, в Началах Евклида материалом для построения доказательств служил человеческий язык. Язык- неуловимая, зыбкая среда хитросплетенных отношений и смыслов с огромным множеством невидимых ловушек. Что же тогда служит конструкционной опорой в Началах? Можно ли утверждать, что все здание выводов поддерживается жесткими структурными элементами или в нем имеются конструкционные слабости и просчеты?
Каждое слово, которое мы используем, наделено для нас смыслом, который и руководит нами, когда мы его применяем.

РИС 21. Вавилонская башня, М. C. Escher (гравюра на дереве, 1928).

Чем обыденнее, чем чаще употребляется слово, тем больше ассоциаций мы имеем с этим словом и тем глубже скрыты корни его содержания.
Поэтому когда кто-то дает определение для широко употребляемого слова в надежде, что мы останемся в его рамках, то это неизбежно приведет к тому, что мы не будем пользоваться предложенным определением, но будем вместо этого руководствоваться (в значительной степени подсознательно) тем, что наш ум выхватит из подвалов своих ассоциаций. Я упоминаю об этом потому что это разновидность проблемы, которую Евклид создал в своих Началах, делая попытку дать определение обычных, широко употребляемых слов типа "точка", "прямая линия", "окружность" и т.д. Как вы можете определить что-то такое, о чем каждый уже имеет ясное представление? Единственный способ - указать, что ваши слова, как предполагается, являются техническими терминами и их нельзя путать с каждодневным значением этих слов, которые только похожи на них по звучанию. Хорошо. Евклид не делал этого, потому что он чувствовал, что точки и линии его Начала были в действительности точками и линиями реального мира. Поэтому не будучи уверенным что все посторонние ассоциации были рассеяны Евклид приглашал читателей позволить своим ассоциациям возникать свободно. . .

Это выглядит почти анархией и не совсем справедливо по отношению к Евклиду. Он записывал аксиомы или постулаты, которые, как предполагал, использовались в доказательствах утверждений. Фактически, ничего другого кроме тех аксиом и постулатов, как он надеялся, не использовалось. Но в этом он ошибался. Неизбежным последствием использования им обычных слов было то, что некоторые из образов вызванных теми словами прокрались в доказательства, которые он создавал. Однако если вы читаете доказательства в Началах, то не увидите явных "скачков" в рассуждениях. Напротив они очень тонкие. Евклид был проницательный мыслитель и не сделал никаких явных ошибок. Тем не менее, дыры там имеются, тем самым, вызывая некоторый дефицит строгости в этой классической работе. Но на это не стоит жаловаться. Нужно просто различать абсолютную строгость и относительную строгость рассуждений. В конце концов, недостаток у Евклида абсолютной строгости послужил причиной некоторых из наиболее плодотворных нововведений в математике спустя более чем две тысячи лет после того как он написал эту работу.
Евклид установил пять постулатов, которые нужно использовать как "абсолютное основание" бесконечного небоскреба геометрии, в котором его Начала составляют только первые несколько сот этажей. Первые четыре постулата довольно краткие и изящные.

(1) Отрезок прямой линии может быть прочерчен, если соединить две точки.

(2) Любой отрезок прямой линии может быть неопределенно долго продлено вдоль нее.

(3) Дан некоторый отрезок прямой линии. Окружность может быть построена, если иметь отрезок как радиус и одну точку на конце отрезка использовать как центр.

(4) Все прямые углы конгруэнтны.

Пятый постулат, однако, не разделяет изящества братьев:

(5) Если проведены две линии, которые пересекаются третьей линией таким образом, что сумма внутренних углов на данной стороне меньше чем два прямых угла, тогда эти две прямых линии неизбежно должны пересечься друг с другом на этой стороне, если их продолжить неопределенно долго .

Хотя он никогда этого явно и не говорил, но Евклид рассматривал этот постулат как ниже утверждение рангом по отношению к другим, потому что он не использовал его в доказательствах первых двадцати восьми утверждений. Таким образом, первые двадцать восемь утверждений принадлежат тому, что могло бы называться "геометрия с четырьмя постулатами" - та часть геометрии, которая может быть получена на основании первых четырех постулатов Начал без помощи пятого (ее также, часто называют "абсолютной геометрией"). Конечно, Евклид скорее предпочел бы вывести этого "гадкого утенка" из остальных постулатов, чем принимать его. Но он не нашел для него никакого доказательства и вынужден был принять как постулат.

Но последователи Евклида не испытывали никакого счастья от необходимости принимать пятый постулат. на протяжении столетий, невероятное число людей тратили невероятное число лет своей жизни в попытке доказать, что пятый постулат был сам по себе результат первых четырех постулатов геометрии. В 1763 году, по крайней мере, двадцать восемь различных доказательств этого были изданы. И все -ошибочные! Все были раскритикованы в диссертации Клигела (G. S. Kliigel). Эти ошибочные доказательства смешивали каждодневную интуицию и строго формальные свойства.
Смело можно сказать, что сегодня едва ли любое из этих "доказательств" составляет какой либо математический или исторический интерес. Но есть и исключения.

Многоликий Неэвклид

Гилорамо Сакчери (Girolamo Saccheri 1667-1733) жил приблизительно в то же время что и Бах. Он имел амбиции освободить геометрию Евклида от недостатков. Основываясь на некоторых более ранних работах, сделанных им в логике, он решил попробовать новый подход к доказательству знаменитого пятого постулата. Предположим, что вы принимаете противоположное ему утверждение, и работаете с ним как с пятым постулатом. . . Естественно, что через некоторое время вы придете к противоречию. Так как никакая математическая система не может содержать противоречие, вы тем самым докажете необоснованность предложенного вами постулата и как следствие - обоснованность пятого постулат Евклида. Мы не станем здесь рассматривать подробности. Удовлетворимся тем, что сообщим: с большим мастерством Сакчери выстроил утверждение за утверждением в рамках "геометрии Сакчери" и в конце концов это его утомило. В какой-то момент ему показалось, что он получил утверждение, которое "противоречило природе прямых линий". Именно это, как он надеялся, и есть давно разыскиваемое противоречие. Здесь он принял решение издать свою работу под названием "Евклид, свободный от всех слабых мест" и на этом иссяк.
Но сделав так, он лишил себя большой посмертной славы, так как он невольно обнаружил то, что открылось позже, названное в последствии "гиперболическая геометрия". Пятнадцатью годами после Сакчери, Ламберт (J. H. Lambert) тоже "прошел мимо цели", на сей раз, пройдя даже ближе. Прошел мимо настолько близко, насколько это было возможно. Наконец сороками годами позже Ламберта и девяносто годами после Сакчери неэвклидова геометрия была признана тем чем она есть. Ее одновременно, как это необъяснимо бывает, открыл венгерский математик Йохан Больяи (Johann Bolyai) в возрасте 21 год и русский математик Николай Лобачевский, которому исполнилось тридцать. По иронии судьбы в этот же год великий французский математик Андран-Мари Легандр (Adrien-Marie Legendre) придумал то, что, как он был уверен, было доказательством пятого постулата Евклида, очень близкое к тому, что предложил Сакчери.
Кстати отец Больяи, Вольфган Больяи (Wolfgang Bolyai), близкий друг великого Гаусса, вложил много сил в попытку доказать пятый постулат Евклида. В письме своему сыну Йохану он пробовал отговорить его от размышлений над этим вопросом:

Ты не должен и пытаться подходить к вопросу о параллельных. Я прошел этот путь до конца. Я пересек эту безграничную ночь, которая погасила весь свет и всю радость моей жизни. Я умоляю тебя оставить вопрос о параллелях в покое. . . я думал, что смогу пожертвовать собой ради истины. Я был готов стать мучеником, который исправит порок геометрии и вернет ее очищенной человечеству. Я выполнил чудовищную, огромную работу. Мои результаты гораздо лучше, чем у других. И все же я не достиг полного удовлетворения. Истина в том, что si paullum a summo discessit, vergit ad imum. Я повернул обратно, когда увидал, что никто не может достигнуть той стороны этой ночи. Я повернул обратно безутешный, полный жалости к всему человечеству. . . я путешествовал минуя все рифы этого адского Мертвого Моря, но всегда возвращался со сломанной мачтой и порванным парусом. Руины моих позиций и моя старость - все, что я имею в итоге. Я неосмотрительно рискнул своей жизнью и Caesar aut nihil.

Но позже, когда его не переубежденный сын действительно имел "кое что", он убеждал его издать результаты не мешкая, напоминая об одновременном появления правильных результатов, столь часто случающихся в мире научных открытий:

Когда наступает время для некоторых вещей, они появляются в самых разных местах на манер фиалок, пробивающихся повсюду ранней весной.

Насколько же это было справедливо в случае неэвклидовой геометрии! В Германии непосредственно Гаусс и некоторые другие исследователи более-менее независимо друг от друга натолкнулись на неэвклидовы идеи. В частности, адвоката Швейкарта (F. K. Schweikart) в 1818 году послал Гауссу страницу описывающую новую "астральную" геометрию. Племянник Швейкерта, Тауринус (F. A. Taurinus) создал неэвклидову тригонометрию, а студент Гаусса, Ваштер (F. L. Wachter), который умер в 1817 году, в возрасте 25-ти лет, нашел некоторые глубоких результата в неэвклидовой геометрии.
Ключ к неэвклидовой геометрии - "прямые рассуждения" относительно высказываний, которые появляются в конструкциях подобных геометриям Сакчери и Ламберта. Высказывания Сакчери "противоречат свойствам прямых линий" только если вы не можете освободить себя от предвзятого понимания того, что должна означать "прямая линия". Если же вы сможете избавить себя от этих предвзятых образов и просто позволите "прямой линии" быть чем-то, что удовлетворяет новым суждениям, то вы достигли радикально новой точки зрения.

Неопределенные термины

Это для нас знакомо. В частности, это возвращает нас к pq-системе и ее варианту, в котором символы приобретают пассивное значение в зависимости от их ролей в теоремах. Символ q особенно интересен, после того, как его "значение" было заменено с добавлением новой схемы аксиом. Аналогичным способом можно позволить и смыслу терминов "точка", "прямая" и так далее, определяться набором теорем (или суждений) в которых они встречаются. Этот способ был великолепно реализован исследователями неэвклидовой геометрии. Они нашли различные виды неэвклидовых конфигураций, отвергая пятый постулат Евклида различными способами и рассматривая последствия такого шага. Строго говоря, они (и Сакчери тоже) не отрицали пятый постулат непосредственно. Они отрицали эквивалентный постулат, который звучит следующим образом:

Дана любая прямая и точка расположенная не на этой прямой. Существует одна и только одна прямая линия, которая проходит через эту точку и никогда не пересекает первую прямую независимо от того, как далеко они простираются.

Вторая прямая линия, как считается, параллельна первой. Если вы утверждаете, что никакой такой линии не существует, то вы получите эллиптическую геометрию, если вы утверждаете что, по крайней мере, две таких линии существуют, то вы получите гиперболическую геометрию. Кстати, причина что такие разновидности все еще называются "конфигурациями" в том, что основной элемент остается неизменным - четыре первых постулата геометрии остаются основной частью любой из геометрий. Присутствие минимального ядра делает для разума восприятие их свойств как свойств хоть и некоторого особого вида, но все же геометрического пространства, даже если это пространство не столь интуитивно понятно как обычное пространство.

Фактически, эллиптическая геометрия легко визуализируется. Все "точки", "прямые" и так далее должны быть частями поверхности в форме "сфера". Я буду писать "ТОЧКА" если я имею в виду специальное значение этого термина, и позвольте писать "точка", когда предпочтителен обыденный смысл. Тогда мы можем сказать, что ТОЧКА состоит из пары диаметрально противоположных точек сферы. ПРЯМАЯ - большая окружность на сфере (окружность, подобная экватору, которая имеет центр в центре сферы) В такой интерпретации высказывания эллиптической геометрии содержат слова типа "ТОЧКА" и "ПРЯМАЯ" и говорят о "продвижении на" поверхности сферы так же как о продвижении на плоскости. Обратите внимание, что две ПРЯМЫЕ пересекаются в двух строго диаметрально противоположных точках на сфере, то есть строго в одной единственной ТОЧКЕ! И так же как две ПРЯМЫЕ определяют ТОЧКУ, так и две ТОЧКИ определяют ПРЯМУЮ.
Рассматривая слова типа "ТОЧКА" и "ПРЯМАЯ" так, как будто они имеют только тот смысл, который скрыт в суждениях из которых эти термины происходят, мы предпринимаем шаг к полной формализации геометрии. Первый шаг. Ведь эта полу-формальная версия все еще использует много слов на обычном языке с их обыденным значением (слова типа "на", "если", "и", "соединить", "содержит"). Обыденный смысл было изгнан из слов типа "ТОЧКА" и "ПРЯМАЯ" и в отличии от остальных терминов, следовательно, они называются неопределенными терминами. Неопределенные термины подобно символам p и q pq-системы становятся определенными в некотором смысле неявно, в совокупности всех тех суждений, где они встречаются, быстрее, чем в любом явном определении.
Можно утверждать, что полное определение неопределенных терминов находится исключительно в постулатах и с момента, как суждения следуют из них, смысл терминов неявно присутствуют уже там. Такое представление говорило бы что постулаты - это неявное определение всех неопределенных терминов, определяемое другими неопределенными терминами.

Возможность различной интерпретации

Полная формализация геометрии совершила бы решительный шаг если бы сделать каждый термин неопределенным, то есть превратить каждый термин в "бессмысленный" символ формальной системы. Я взял в кавычки "бессмысленный" потому что, как вы знаете, символы автоматически приобретают пассивный смысл в соответствии с теоремами, в которых они встречаются. Это конечно, другой вопрос, обнаруживают ли люди этот смысл, как это требуется, во всем множестве идей, который может быть связан изоморфизмом в символах формальной системы. Если начинать с идеи формализации геометрии, то, по-видимому, в ней имеется такая определенная интерпретация каждого символа, что их пассивное значение было включено в систему. Именно это я делал для p и q, когда начал создавать pq-систему.

Но может иметься другой пассивный смысл, который является вполне заметным, однако который все же никто не заметил. Например, имеются удивительные интерпретации символа p как "равно, если" и символа q как "отнять из" в первоначальной pq-системе. Хотя это довольно тривиальный пример, в этом скрыта суть идеи, что символы могут иметь много смысловых интерпретаций в зависимости от наблюдателя, который их устанавливает.
Теперь можно суммировать наши наблюдения по поводу слова "непротиворечивость". Мы начали наше рассуждение, получив то, что, казалось, противоречит формальной системой - внутренне противоречит и противоречит с внешним миром. Но секунду спустя мы все расставили по местам, когда обнаружили свою ошибку: мы выбрали неудачную интерпретацию для символов. Изменив интерпретацию, мы восстановили последовательность системы! Теперь становиться ясным. Что последовательность (или непротиворечивость) не является собственным свойством формальной системы само по себе, а зависит от интерпретации, которую предлагают для нее. Из тех же самых соображений выходит, что противоречивость несвойственна любой формальной системе.

Разновидности непротиворечивостей

Мы говорили относительно "последовательности" и "непоследовательности", без того, чтобы определить, что это такое. Мы положились на добрые, старые, обыденные понятия. Но теперь определим точно, что предполагается под последовательностью или непротиворечивостью формальной системы (вместе с интерпретацией): это если каждая теорема, когда она интерпретируется, становиться истинным утверждением. И мы будем говорить, что противоречивость возникает тогда, когда, по крайней мере, есть хотя бы одно ложное утверждение среди интерпретируемых теорем.

Но это определение, кажется, говорит относительно противоречивости с внешним миром. Что же относительно внутренних противоречий? Возможно, система была бы внутренне противоречивой, если бы она содержала две или более теоремы, чьи интерпретации были несовместимы друг с другом, и внутренне последовательна, если все интерпретируемые теоремы были совместимы друг с другом. Рассмотрим, например, формальную систему, имеющую всего три теоремы: TbZ, ZbE, и EbT. Если Т интерпретировать как "Черепаха" Z как "Зенон", Е как "Эгберт", а ' x b y' , интерпретировать, как "x всегда побеждает в шахматах y", то мы имеем следующую интерпретацию теорем:

Черепаха всегда побеждает в шахматах Зенона.
Зенон всегда побеждает в шахматах Эгберта.
Эгберт всегда побеждает в шахматах Черепаху

Утверждения не несовместимы, хотя они описывают довольно причудливый круг шахматистов. Следовательно, в этой интерпретации, формальная система, в которой эти три цепочки символов являются теоремами, внутренне последовательна, хотя, фактически, ни одно из этих утверждений не является истинным! Но внутренняя последовательность не требует, чтобы все теоремы получились истинными. Просто они должны быть совместимы друг с другом.

Теперь предположите вместо этого, что ' x b y' надо интерпретировать, как "х был изобретен у". Тогда мы имели бы:

Черепаха был изобретен Зеноном.
Зенон был изобретен Эгбертом.
Эгберт был изобретен Черепахой.

В этом случае не имеет значения, является ли каждое отдельно взятое утверждение истинным или нет. Возможно, нет никакого способа узнать какое из них ложно, а какое - правда. Но в чем можно быть, однако, уверенным, это в том, что не все они могут быть истинными одновременно. Таким образом, эта интерпретация делает систему внутренне противоречивой. Эта противоречивость зависит не от интерпретации этих трех заглавных букв, но от интерпретации символа b и из факта, что эти три литерала циклически переставлены вокруг связки b. Таким образом, можно обнаружить внутреннюю противоречивость, не интерпретируя все символы формальной системы (в данном случае достаточно было интерпретировать один единственный символ). К тому моменту, когда достаточно много символов уже получили интерпретацию, может выясниться, что нет никакого способа, которым бы остальная часть символов могла бы быть интерпретирована так, чтобы все теоремы получились истинными. Но это не только вопрос истины и лжи - это вопрос возможностей. Все три теоремы вышли бы ложными, если заглавные буквы интерпретировались бы как названия реальных людей. Но не в этом причина, почему мы назвали систему внутренне противоречивой. Основанием для этого были циклическая зависимость символа b при такой интерпретации (Кстати, вы найдете больше об этом треугольнике авторов в главе XX).

Гипотетические миры и противоречивость

Мы показали два способа смотреть на последовательность (непротиворечивость): первый говорит что "система плюс интерпретация" согласуется с внешним миром, если каждая теорема получается истинной при интерпретации. Второй способ говорит, что "система плюс интерпретация" является внутренне последовательной, если все теоремы получаться взаимно совместимыми при интерпретации. Имеется близкая связь между этими двумя типами последовательностей. Чтобы определить являются ли некоторые высказывания взаимно-совместимыми, вы пробуете представить себе мир, в котором все они могут быть одновременно истинными. Поэтому внутренняя непротиворечивость зависит от непротиворечивости с внешним миром только теперь "внешнему миру" позволено быть любым воображаемым миром, вместо того, в котором мы живем. Но это чрезвычайно неопределенное и неудовлетворительное решение вопроса. Что представляют собой "воображаемые миры"? В конце концов, можно вообразить миры, в которых три персонажа циклически изобретают друг друга. Или нет? Возможно ли, изобрести мир, в котором имеются квадратные круги? Можно ли вообразить мир, в котором правят законы механики Ньютона, а не относительность? Возможно ли вообразить мир в котором зеленое одновременно может быть не зеленым? Или мир, в котором животные состоят не из клеток? Представим ли мир, в котором Бах импровизирует фугу с восемью частями на тему короля Фридриха Великого? А мир, в котором москиты являются более умными, чем люди?
Можно ли представить мир, в котором черепахи могут играть фуги или разговаривать?!
Черепаха, играющая в футбол, это было бы слишком, конечно. . .

Некоторые из этих миров кажутся более реалистичными чем другие, в то время как некоторые, кажется, воплощают в себе логические противоречия. Например, зеленый и не зеленый. В то время как некоторые кажутся (не имея лучшего слова) "вероятными". Типа того мира, где Бах импровизирует фуги из восьми частей или мир где животные не состоят из клеток. Или даже, задумайтесь об этом, мир, в котором законы физики должны быть другими. Грубо говоря, тогда должна установиться другие стандарты непротиворечивости. Например, наиболее мягкой была бы "логическая последовательность", которая не накладывала бы на объекты никаких ограничений, кроме логических. Более точно: "система плюс интерпретация" была бы логически последовательны для нас, до тех пор, пока любая из двух ее теорем не противоречат друг другу при интерпретации, математически последовательны до тех пор, пока интерпретируемые теоремы не нарушают математику, физически последовательны пока интерпретируемые теоремы совместимы с законами физики. За этим следуют биологическая непротиворечивость и так далее. В биологически последовательной системе имелись бы теорема, чья интерпретация гласила бы "Шекспир написал оперу" но не содержала бы никакой теоремы, интерпретация которой гласила: "существуют животные меньше клетки". Вообще говоря, такого рода фантастическая противоречивость не изучаются по причине невообразимой хитросплетенности уровней утверждений. Какая противоречивость, например, можно сказать, возникает в проблеме трех персонажей, где неясно кто кого изобретает?
Логическая? Физическая? Биологическая? Литературная?
Обычно граница между интересной и неинтересной областью пролегают между физической и математической непротиворечивостью (конечно, математики и логики, которые ее проводят, вряд ли беспристрастная судейская команда. . ..) Это значит, что виды противоречий, которые "учитываются" для формальных систем, являться только логического и математического типа. Но и по этому соглашению мы все же нашли интерпретацию, которая делает трио теорем TbZ, ZbE, EbT противоречивым. Мы можем делать такую интерпретацию для b : "является больше чем". Что можно сказать в отношении T, Z и E? Они могут интерпретироваться как натуральные числа, например Z как 0, T как 2 и E как 11. Заметьте, что две теоремы получаться в этом случае истинными, а одна - ложная. Если бы мы вместо этого интерпретировали Z как 3, то мы имели бы два ложных высказывания и только одно истинное. Но в любом случае мы имели бы противоречие. Фактически, значения, присвоенные T, Z и E неприменимы (нерелевантные) пока мы подразумеваем под ними только натуральные числа. В очередной раз мы видим, что необходима только часть интерпретации, чтобы признать внутреннюю противоречивость.

Одна формальная система внутри другой

В предыдущем примере некоторые символы могли иметь интерпретацию, в то время как другие не имели. Это напоминает нам об описании геометрии на естественном языке с использованием некоторых слов как неопределенных терминов. В таком случае все слова разделяются на два класса: те, чье значение установлено и неизменно и те, которые должны быть уточнены для выяснения непротиворечивости системы (они - неопределенные термины). Построение геометрии таким способом требует, чтобы смысл терминов был уже установлен на более высоком уровне где-то за пределами геометрии. Эти слова составляют жесткий скелет, образуют основной каркас системы, который потом заполняется другим материалом и который можно, при желании, заменить (Евклидова или неэвклидова геометрия).

Формальные системы часто выстраиваются именно в такой иерархической или упорядоченной манере. Например, Формальная Система I могла бы быть выстроена с правилами и аксиомами, которые дают уверенность предполагать пассивное значение ее символов. Теперь, допустим Формальная, Система I. включается полностью в большую систему, систему с бол'ьшим количеством символов - Формальную систему II. Тогда правила и аксиомы Формальной Системы I являются частью правил и аксиом Формальной системы II. Пассивное значение символов Формальной Системы I остается действительными, остаются ее формой и неизменным скелетом, который играет большую роль в определении пассивного смысла (значения) новых символов в Формальной Системе II. Вторая система, в свою очередь, может служить скелетом третьей системе и так далее. Это вполне возможно и геометрия - хороший этому пример. Иметься система (та же, Абсолютная геометрия) которая частично выявляет пассивное значение неопределенных терминов, а некоторые другие могут быть добавлены дополнительными правилами и аксиомами, которые в дальнейшем ограничивают пассивные значения неопределенных терминов. Все происходит так, как происходит с евклидовой и неэвклидовой геометрией.

Фрагменты стабильности в визуальном пространстве

Подобным иерархическим способом мы приобретаем новые знания, новые слова, ощущаем, что объект нам незнаком. Это особенно интересно в случае восприятия рисунков Эшера, типа Относительности (рис 22), внутри которых находятся невозможные объекты. Вы можете представить как мы делаем самые разные интерпретации, давая иное толкование картине раз за разом, пока не найдем интерпретацию всех ее частей, свободную от взаимных противоречий. Но наши попытки бесплодны. Мы смотрим на это озадаченные и удивленные. Мы озадаченны лестницами, по каждой из которых движутся люди в направлении, противоречащих каждой отдельно взятой лестнице. Эти лестницы -"острова уверенности" на которых мы базируем нашу интерпретацию полной картины. Однажды идентифицировав такой остров, мы пробуем расширить наше понимание, пытаясь установить отношения, в которых они находятся друг к другу. Но в этих попытках мы сталкиваются с неприятностью. Если мы сделаем попытку отступить, то есть подвергнуть сомнению "острова уверенности", то мы так же столкнемся с неприятностью, но другого рода. Нет никакого способа ухватиться за задний плана, и причина этого они же - лестницы. Они не рыба, не плеть не ладонь - они всего лишь лестницы. ( Имеется еще одна возможность - оставить все линии на картине полностью не интерпретированными подобно "бессмысленным символам" формальной системы. Этот единственный спасительный путь и является примером U-способа. Дзен-подходом к символам)

Рис. 22 Относительность, М. C. Escher (lithograph, 1953).

В итоге мы вынуждены по иерархическому характеру нашего процесса мышления видеть или сумасшедший мир или только сплетение бессмысленных линий. Подобный анализ можно было бы сделать для многих картин Эшера, которые опираются на представления некоторых основных форм, расположенных нестандартным образом и наблюдатель видит парадокс на высоком уровне. Но отступать уже слишком поздно. Он не может вернуться и изменить свое мнение относительно того, как интерпретировать объекты низшего уровня. Различие между рисунками Эшера и неэвклидовой геометрией то, что в геометрии разумная интерпретация может быть найдена для неопределенных терминов в результате постижения всей системы, в то время, как для творений Эшера окончательный вывод не совместим ни с какой возможной реальностью, независимо от того как долго каждый будет смотреть на картину. Конечно, можно все еще выдумывать фантастические миры в которых Эшеровские трюки могут происходить. . . Но в таких мирах законы биологии, физики, математики или даже логики будут нарушены на одном уровне в то время как на другом они продолжают спокойно исполняться, что придает этим мирам крайнюю сверхъестественность (Пример этого - Водопад (рис5) , где нормальное тяготение действует на перемещение воды, но природа пространства нарушена)

Одинакова ли математика в любом из мыслимых миров?

Только что мы подчеркнули изложенный выше факт, что внутренняя непротиворечивость формальной системы (вместе с интерпретацией) требует чтобы имелся некоторый вообразимый мир где это возможно, то есть мир, ограниченный только тем, что математика и логика в нем такие же самые, как и в нашем мире. В таком мире все интерпретируемые теоремы должны быть истинными. Внешняя непротиворечивость, однако (последовательность с внешним миром) требует, чтобы все теоремы вышли истинными в реальном мире. В особом случае, когда есть желание выстроить последовательную систему, чьи теоремы должны интерпретироваться только как утверждения математики, то казалась бы, что различие между двумя типами последовательности должны исчезнуть. С этого момента, согласно тому, что мы сказали, все воображаемые миры имеют ту же математику что и реальный мир. В каждом мыслимом мире 1 плюс 1 должно равняться 2, аналогично должно иметься бесконечное число простых чисел. Кроме того, в каждом из мыслимых миров, прямые углы должны совпадать, и конечно через любую точку не на данной линии можно провести одну и только одну параллельную линию...
Но минуточку! Но это же постулат о параллельных и утверждать, что он универсален было бы ошибкой в связи с тем, что мы уже знаем. Если все воображаемые миры повинуются постулату о параллельных, то тем самым мы утверждаем что неэвклидова геометрия невозможна. Это возвращает нас назад, к тем же представлениям что исповедовали Сакчери и Ламберт. Это неблагоразумно. Но что же получается? Не вся математика одинакова в любом из мыслимых миров? А может под подозрением и сама логика? Представимы ли миры, где противоречия - норма существования? Миры, где противоречие- не противоречия?
Хорошо. В некотором смысле, просто фантазируя, мы показали что такие миры являются действительно мыслимыми, но в более глубоком смысле они все же очень невообразимы ( это само по себе небольшое противоречие). Весьма важным, однако, представляется следующее: если мы хотим иметь возможность связать воедино все в нашем воображаемом мире, мы должны принять некоторую общую основу и это должно изрядно включать логику. (Имеются системы вероисповедания, которые отклоняют такую точку зрения, пологая ее слишком логической. В частности, Зен включает в себя как противоречия, так и непротиворечивые факты в равной мере. Это может казаться непоследовательным (противоречивым), но если непоследовательность тоже часть вероисповедания, то что можно еще возразить?)

Является ли теория чисел одной и той же во всех мыслимых мирах?

Если мы предполагаем что логика должна быть неотъемлемой частью любого воображаемого нами мира (и обратите внимания, мы не имеем в виду какую-то двойную логику, но в следующих главах мы встретим и это) то что из этого? Действительно ли можно представить, что в некоторых из миров нет бесконечного числа простых чисел? Кажется ли столь необходимыми, чтобы числа повиновались одним и тем же законам во всех мыслимых мирах? Или о концепции "натуральное число" лучше думать как о неопределенном термине подобно "ТОЧКА" или "ПРЯМАЯ"? В этом случае теория чисел была бы бифуркационной (разветвляющейся) теорией . Подобно геометрии имелись бы стандартные и нестандартные теории чисел. Но тогда должен был бы существовать некий аналог абсолютной геометрии: "базовая" теория, инвариантный компонент всех теорий чисел, которая бы идентифицировала бы каждую теорию как теорию чисел в большей степени, чем скажем теорию бананов или каучука. В настоящий момент, кажется, достигнуто согласие современных математиков и философов, что имеется такая теория чисел, которую наряду с логикой нужно бы включить в то, что мы подразумеваем под "мыслимыми мирами". Это ядро теории чисел, аналогия абсолютной геометрии, называется арифметикой Пеано (Peano) и мы формализуем ее в главе VIII. Так же ( это теперь хорошо установлено как следствие теоремы Геделя) теория чисел действительно является бифуркационной теорией со стандартными и нестандартными версиями. Но в отличии от ситуации в геометрии, число "типов" теорий чисел бесконечно, что делает ситуации значительно сложнее.

Для практического использования все теории чисел - одинаковые. Другими словами, если бы строительство моста зависело от теории чисел (что в некотором смысле так и есть), то факт, что имеются различные теории чисел, не имел бы значения, так как аспекты относящиеся к реальному миру во всех теориях чисел совпадают друг с другом. Нельзя сказать того же самого относительно различных геометрий. Например, сумма углов треугольника 180 градусов только в Евклидовой геометрии, но она больше в эллиптической геометрии и меньше в гиперболической. Известно, что однажды Гаусс попытался измерить сумму углов в большом треугольнике, между тремя вершинами гор чтобы раз и на всегда определить какого вида геометрия в действительности царит в нашей вселенной. Спустя сто лет Эйнштейн создал Общую Теорию Относительности, которая утверждала, что геометрия вселенной определяется содержащейся в ней материей. Так что никакая конкретно геометрия не свойственна пространству непосредственно. На вопрос "Какая геометрия является истинной?" природа дает неоднозначный ответ не только в математике, но и в физике. Что же касается вопроса "Какая теория чисел является истинной?" то мы сможем об этом говорить больше, после прохождения Теоремы Геделя подробно.

Полнота

Если последовательность или непротиворечивость -минимальное условие при котором символы приобретают пассивный смысл, то дополняющим его понятием является полнота, которая является полным и окончательным подтверждением пассивного смысла символов. Если непротиворечивость - это свойство того, что "все что производится системой истинно", то полнота говорит о другом: "каждое истинное утверждение производится внутри системы"
Поясним эти понятия. Мы не подразумеваем (и не можем подразумевать) каждое истинное утверждение в мире. Мы подразумеваем только те, которые принадлежат области, которую пытаемся представить в системе. Поэтому полнота означает:

"Каждое истинное утверждение, которое может быть выражено некоторой записью с помощью символов системы - теорема системы".

Непротиворечивость: когда каждая теорема при интерпретации оказывается истинной (в некотором воображаемом мире).

Полнота: когда все утверждения, которые являются истинными (в некотором воображаемом мире) могут быть выражены в виде цепочек символов системы и являются теоремами.

Пример формальной системы, которая является полной на скромном уровне - первоначальная pq-система с первоначальной интерпретацией. Все истинные утверждения о суммах двух положительных целых чисел представлены теоремами системы. Мы могли бы сказать это по-другому: "Истинность всех утверждений о значении суммы двух положительных целых чисел мы доказываем в пределах системы". (Внимание! Когда мы начинаем использовать термин "доказываемое утверждение" вместо "теорема", это показывает, что мы начинаем стирать различие межу формальной системой и ее интерпретацией. Это нормально, если мы хорошо осознаем туманность термина, и при условии, что мы понимаем, что иногда возможны разные интерпретации). Pq-система в первоначальной интерпретации полна. Она так же непротиворечива (последовательна), так как никакое ложное утверждение (используя нашу новую фразу) не доказуемо в пределах системы.
Кто-то мог бы утверждать, что эта система, мол, не полна на основании того, что сумма трех положительных целых чисел (типа 2+3+4 =9) не представляется теоремами pq-системы, хотя она представима в нотации системы (например: _ _ p _ _ _ p _ _ _ _ q _ _ _ _ _ _ _ _ _). Однако эта цепочка неправильно построена и следовательно должна рассматриваться как абсолютно бессмысленная настолько, насколько бессмысленна цепочка _ pqp _ _ _ qpq . Тройная сумма просто не выражается в нотации системы, так что полнота системы сохраняется.
Несмотря на полноту pq-системы в этой интерпретации, она, конечно, слишком далека от окончательного завоевания всей истины в теории чисел. Например, не имеется никакого способа, каким бы pq-система сообщила нам, сколько существует простых чисел. Теорема Геделя о неполноте говорит, что любая система, которая является "достаточно мощной", именно из за своей мощи является неполной. Это значит, что там есть правильно построенные цепочки, которые выражают истинные утверждения теории чисел, но которые не являются теоремами ( имеются истины в теории чисел, которые не доказуемы в пределах системы). Системы, подобные pq-системе, являются полными, но не очень мощными. Они что-то наподобие фонографов с низким качеством звучания. Эти системы настолько бедны изначально, что становиться очевидным: они не могут нас удовлетворить, они не могут сообщить нам все, что мы хотели бы знать относительно теории чисел.

Как интерпретация разрушает или восстанавливает полноту

Что я имел в виду, когда говорил, что "полнота это полное и окончательное подтверждение пассивного смысла"? Это означает, что если система построена, но она неполна, то имеется несоответствие между символами и их интерпретацией. Система не имеет мощности оправдать себя, будучи интерпретирована таким образом. Иногда, если интерпретация немного "урезана", система может стать полной. Чтобы иллюстрировать эту идею, давайте посмотрим на измененную pq-систему (использующую вторую схему аксиом) и ее новую интерпретацию, которую мы применили для нее.
После изменения pq-системы мы изменили и интерпретацию для q с "равняется" на "больше чем или ровно". Мы видим, что измененная pq-система была последовательна в такой интерпретации и все же что-то здесь не так. Проблема проста: имеется теперь много выраженных в нотации системы истин, которые оказываются не теоремами. Например "2 плюс 3 больше чем или равно 1" выражено не теоремой _ _ p _ _ _ q _ . Интерпретация слишком свободная! Она не очень аккуратно отображает то, что теоремы делают в системе. В такой широкой интерпретации pq-система неполна. Мы могли бы восстановить ситуацию или (1) добавлением новые правил к системе, делая ее более мощной или (2) сузив интерпретацию. В этом смысле разумным кажется выбрать второй путь - ужать интерпретацию. Вместо интерпретации q "больше чем или равно". Мы должны использовать "равняется или больше на 1". Теперь система становиться и последовательной и полной. И полнота подтверждает справедливость (уместность) интерпретации.

Неполнота формальной теории чисел

В теории чисел мы столкнемся с неполнотой снова. Но там, чтобы исправить ситуацию, нас будут влечь в другую сторону - к добавлению новых правил, то есть мы будем стремиться сделать систему еще более мощной. Ирония в том, что всякий раз, когда мы добавляем новые правила, мы думаем, что вот теперь уже мы сделаем систему полной. И характер данного безвыходного положения можно иллюстрировать следующей аллегорией. . .
Вы имеете проигрыватель и имеете грамзапись, которая, в порядке рабочей гипотезы, помечена как "Канон B-A-C-H". Однако, когда мы играем эту грамзапись на проигрывателе, вынужденные обратной связью колебания (как это случалось с записями Черепахи) вмешиваются настолько сильно, что мы не можем уловить на фоне этих помех мелодию. Тогда мы приходим к заключению, что что-то из двух дефектное. Или наша грамзапись или наш проигрыватель. Что бы проверить нашу грамзапись, мы должны прослушать ее на проигрывателе друзей и услышать качество звучания. Чтобы проверить проигрыватель, мы должны поставить на него какую-либо грамзаписи друзей и убедиться соответствует ли звучание тому, что написано на этикетке. Если наш проигрыватель пройдет это испытание, то мы скажем, что грамзапись дефектна. Наоборот, если грамзапись пройдет испытание, то мы скажем, что проигрыватель дефектный. Но что мы можем сказать, если оба пройдут соответствующие испытания? В этом случае стоит вспомнить цепь двух изоморфизмов (рис. 20) и тщательно думать!