World Wide GEB

GEB
Дуглас Р. Хофштадтер.
[ предыдущая ] [ оглавление ] [ следующая ]

Перевод Александра Семенова

Г Л А В А III
Фигура и Фон

Простые числа против составных

Есть что-то странное в идее, что мысль, во всем своем многообразии, может быть воспроизведена простыми типографскими манипуляциями. Единственная пока нами удачно воспроизведенная таким образом идея - это идея суммирования, и в этом нет ничего странного. Но предположим, что наша цель - создать формальную систему с теоремами формы Px где символ x - это цепочка дефисов и теоремами были бы только те цепочки, у которых количество дефисов - простое число. То есть P_ _ _ была бы теоремой, а P_ _ _ _ - нет. Как это можно было бы сделать типографскими способом?
Сначала, важно четко определить, что мы понимаем под типографскими действиями. Полный набор таких действий мы могли видеть в MIU-системе и pq-системе, так что нам только осталось привести список этих действий:

(1) читать и распознавать любой символ из конечного множества (алфавита);
(2) писать любой символ, принадлежащий к этому множеству;
(3) копировать любой из этих символов из одного места в другое;
(4) стирать любой из выбранных символов;
(5) сравнивать два символа, стоящие в разных местах;
(6) хранить и использовать список ранее произведенных теорем.

Этот список немного избыточен, но это не важно. Важно, что здесь ясно видно - используются только элементарные возможности. Каждая из них гораздо проще, чем способность отличить простое число от составного. Как же тогда мы можем скомбинировать некоторые из этих действий, чтобы построить формальную систему, которая разделяет простые числа от составных?

Tp-система

Первым шагом к достижению этой цели может стать решение более простой, но связанной с этим задачи. Мы можем попробовать сделать систему, подобную pq-системе, за исключением того, что в ней отображается умножение, а не сложение. Давайте назовем ее Tq-системой, t - 'times' - кратность. Более определенно: предположим X, Y и Z - это соответственно число дефисов в x, y и z - цепочках из дефисов. (Заметьте. Я использую различное написание для того, чтобы отличить число дефисов в цепочках и наименование самих цепочек.) Тогда мы признаем цепочку x t y q z теоремой, если X, умноженное на Y, равняется Z. Например _ _ t _ _ _ p _ _ _ _ _ _ должна быть теоремой, так как 2 умноженное на 3 дает 6. Но _ _ t _ _ _ p _ _ _ не должна быть теоремой. Tp-система может быть описана примерно так же легко, как и pq-система, а именно: используя только одну схему аксиом и только одно правило вывода:

Схема аксиом: x t _ q x аксиома, всякий раз, когда x -цепочка дефисов.

Правило вывода

x, y

y _

Ниже показан вывод теоремы _ _ t _ _ _ p _ _ _ _ _ _

(1) _ _t _ q _ _ .....................(Аксиома)
(2) _ _ t_ _ q _ _ _ _ ........... (По правилу вывода, используя (1) как старую теорему)
(3) _ _ t_ _ _ q _ _ _ _ _ _ .. (По правилу вывода, используя (2) как старую теорему)

Обратите внимание - средняя цепочка дефисов увеличивается на один дефис при каждом применении правила вывода, поэтому легко предсказать, что если вы хотите получить теорему с 10-ю дефисами в середине, то вы примените правило вывода девять раз подряд.

Покорение сложных

Теперь и умножение (несколько более хитрая идея, чем сложение) тоже "поймана" в сети типографских символов подобно птицам на гравюре Эшера "Освобождении". Ну а что же с простыми числами? У нас есть план, который кажется блестящим: используя tp-систему определить новое множество теорем формы Cx , которые характеризуют составные (сложные) числа следующим образом:

Правило: предположим, что x, y и z - какие-то цепочки дефисов. Если x_ t y_ q z - теорема. Тогда Cz -теорема.

Это сработает вот почему. Число Z (число дефисов в цепочке z) является составным, если оно есть произведение двух чисел больших чем 1, а именно X+1 (число дефисов в цепочке x_ ) и Y+1 (число дефисов в цепочке y_ ). Я отстаиваю перед вами это новое правило и для этого привожу в оправдание "Интеллектуальный способ". Это потому что вы - человек и хотите знать почему появилось такое правило. Работай вы исключительно в "Механическом режиме", вам не нужны были бы подобные оправдании, так как в M-режиме вы механически следуете правилам, счасливы этим и никогда не станите подвергая сами правила сомнению!

Поскольку вы работает в I-режиме, вы будете все время стремиться стирать в вашем сознании разницу между цепочками и их интерпретациями. Здесь вы видите, что суть происходящего может оказаться весьма запутанной, если вы начинаете чувствовать "смысл" в символах, которыми манипулируете. Придется бороться с собой, постоянно удержать себя от мысли, мол, цепочка '_ _ _' является числом 3. Требование формальности, которое по началу в главе I озадачивало (потому что его требования казались совершенно очевидным) здесь проявляет свою утонченность и становится ключевым. Это очень важная вещь - остерегаться смешивания I-способа с M-способом, иначе говоря, вы должны избегать соблазна и не смешивать арифметические факты с типографскими теоремами.

Ошибка в определении простых чисел

Очень соблазнительно перескочить сразу от теорем C-типа непосредственно к теоремам P-типа, предложив правило следующего вида:

Предложенное правило: Предположим, что x -цепочка дефисов. Тогда если Cx не теорема, тогда Px -теорема.

Фатальный порок этой идеи в том, что проверка Cx на принадлежность к не теоремам - явно не типографское действие. Чтобы знать, что MU не теорема MUI-системы вы должны выйти из системы. . . и точно так же придется поступить для реализации Предложенного правила! Это правило нарушает все каноны формальных систем, оно вынуждает вас работать неформально, то есть вне системы. Конечно, ранее приведенное типографское действие (6) позволяет исследовать запас ранее найденных теорем. Но Предложенное правило просит, что бы вы исследовали гипотетическую "Таблицу Не-теорем". Но что бы получить такую таблицу вы были бы должны делать некоторые рассуждения вне системы. Строить рассуждения, которые показали бы, почему некоторые цепочки не могут быть получены внутри системы. Было бы очень неплохо, если бы имелась другая формальная система, которая может произвести "Таблицу не-теорем" типографскими способом. Фактически наша цель и состоит в том, чтобы найти именно такую систему. Но предложенное правило - не типографское правило и должно быть отброшено.

Это настолько важный момент, что мы могли бы на нем остановиться несколько дольше. В нашей C-системе (которая включает Tp-систему и правило, которое определяет теоремы C-типа) мы имеем теоремы типа Cx где 'х' как обычно - цепочка дефисов. Имеются так же не теоремы формы Cx (они и есть то, что я называю "не-теоремам", хотя конечно tt_Cqq и другой плохо формализованный мусор- не-теоремы тоже). Различие в том, что теоремы имеют составное число дефисов, а не-теоремы - содержат простое число дефисов. Теперь допустим что все теоремы имеют общую "форму" (то есть происходят из общего набора типографских правил). Тогда и все не-теоремы тоже имеют общую "форму" в том же самом смысле? Ниже приведен список теорем C-типа, показанных без их происхождения. Числа в скобках - просто число дефисов в теоремах.

                    C - - - - (4)
                    C - - - - - - (6)
                    C - - - - - - - - (8)
                    C - - - - - - - - - (9)
                    C - - - - - - - - - - (10)
                    C - - - - - - - - - - - - (12)
                    C - - - - - - - - - - - - - - (14)
                    C - - - - - - - - - - - - - - - (15)
                    C - - - - - - - - - - - - - - - - (16)
                    C - - - - - - - - - - - - - - - - - - (18)
                                        *
                                        *
                                        *

"Дыры" в этом списке и представляют собой "не-теоремы". Повторим ранее заданный вопрос: "дыры", в целом, так же имеют форму? Насколько разумно говорить лишь на основании того, что они являются пропусками в списке, мол, они имеют некую общую для всех форму? И да, и нет. То, что они имеют некоторые общие типографские свойства - бесспорно, но хотим ли мы назвать это "форма" - не ясно. Поводом для колебаний является то, что "дыры" только отрицательно (негативно) определены. Они - то, что остались от списка, который был положительно (позитивно) определен.

Фигура и Фон

Здесь стоит вспомнить различие между фигурой и фоном в искусстве. Когда фигура или "положительное пространство" (например портрет человека, живопись, натюрморт) нарисованы внутри рамки, неизбежным следствием становиться то, что его дополнительная форма( "задний план", "фон", "отрицательное пространство") тоже оказывается прорисована. В большинстве картин отношение фигура-фон играют относительно небольшую роль. Художники намного меньше уделяют внимание фону, чем фигуре. Но иногда художники интересуются и фоном тоже.

Существуют красивые алфавиты, которые построены на игре между фигурой и фоном. Ниже приведено сообщение, написанное в таком алфавите. Сначала это послание напоминает нагромождение случайных капель. Но если вы рассматриваете рисунок издалека некоторое время, то внезапно перед вами возникнут семь букв.

Рис. 15

Подобный же эффект можно увидеть, если посмотреть на мой рисунок Дымового Сигнала (рис. 139). По нагромождению линий отгадайте загадку: вы можете как-нибудь выделить контур, содержащий слова и в фигуре, и в фоне?

Позвольте мне теперь специально разделить два вида форм: курсивно прорисованные и рекурсивные. (между прочим, это мои собственные термины и здесь они используются не совсем в обычном смысле). Курсивно прорисованные фигуры те, чей фон - случайный, побочный результат акта рисования. Рекурсивная фигура - та, чей фон может быть замечен как самостоятельная фигура. Обычно такое восприятие преднамеренно провоцируется художником. "Ре" в названии "рекурсивный" означает, что и передний план и фон являются курсивным рисунком. Фигура как бы дважды-курсивна. Каждая граница в рекурсивном рисунке - обоюдоострый меч. М. К. Эшер был мастером в рисовании рекурсивных фигур. Посмотрите, например, на его прекрасное изображение рекурсивных птиц (рис 16).

Рис. 16 Птенцы в полете опираются на птенцов
М. C. Escher ( 1942 из записной книжки)

Но принятая нами классификация изображений не столь строго как в математике. Кто может окончательно сказать, что любой специфический фон не есть фигура? Однажды прорисованный, практически всякий фон представляет интерес сам по себе. В этом смысле каждая фигура рекурсивна. Но это не то, что я вкладывал в смысл этого термина. У нас имеется интуитивное, естественное представление для воспринимаемых нами форм. Является ли и передний план, и фон распознаваемыми формами? Если так, то рисунок рекурсивен. Если вы будете вглядываться в фона большинства картин вы найдете их довольно неузнаваемым. Это значит:

Существуют распознаваемые фигуры, чье отрицательное пространство не является распознаваемой формой. Более технически это звучит так:

Существуют курсивные формы, которые не рекурсивны.

Идея головоломки Скотта Кирна (Scott E Kirn) похожа на ранее упомянутую головоломку, и я назвал ее "ФИГУРО-ФИГУРНАЯ ФИГУРА". Она показано на рис. 17
Если вы настроитесь на восприятие формы черного и белого одновременно, вы будите видеть "ФОРМУ" всюду, а "ФОНА" нигде нет! Это пример рекурсивной фигуры. В этом хитром рисунке есть два не эквивалентных способа воспринимать черные области:

Рис. 17 ФИГУРО-ФИГУРНАЯ ФИГУРА. Скотт Кирн. ( 1975 Scott E Kirn )

отрицательное пространство

трансформированная

(В данном, особом случае "Фигурно-фигурной фигуры" эти два способа оказались эквивалентны. Но в большинстве черно-белых картин этого не произошло бы). Далее, в главе VIII, когда мы создадим нашу Типографскую Теорию Чисел. (TNT - Typographical Number Theory) мы будем надеяться, что множество всех ложных утверждений теории чисел может быть получено двумя аналогичными способами:

отрицательное пространство

трансформирование

Но TNT (тринитротолуол? А. С.) эти надежды разнесет в клочья, потому что:

Вы увидите, почему и как это случилось в главе XIV. Но пока обдумайте ситуацию по схематическому образу представленному на рис. 18.

* Путь некий джин безостановочно производит все теоремы TNT-теории и только их. Но из Теоремы Геделя известно, что в числе тех цепочек, которые никогда не выдаст TNT- джин есть цепочки, которые действительно говорят правду о числах. Джин, конечно, может бесконца ловить нх и заставлять на себя работать (то есть объявит их новыми аксиомами и из них строить теоремы теперь расширенной TNT) Но всегда останутся "вольные" истины. Сколько не лови, всегда будет не охваченная TNT-джином правда о числах. Прим А. С.

** Пускай TNT- джин механически выдает все истинные цепочки TNT. А его слуги быстренько "перекрашивают" их в "черный цвет" и сажают в тюрьму (за то что они лгут). Красят они так: в начало каждой цепочки приписывают символ отрицания (этот символ есть в алфавите TNT). В результате получается множество заведомо ложных цепочек. Однако не все, действительно ложные утверждения о числах окажутся "за решеткой" этого множества. Часть ложных всегда будет гулять на свободе! Прим А. С.

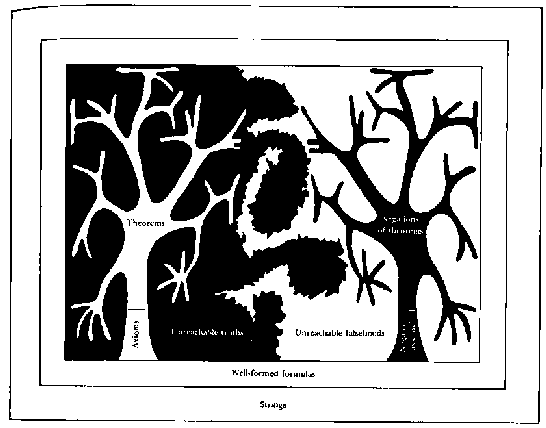
ФИГУРА 18. Здесь визуально, в символической форме, показано отношение между различными классами цепочек TNT. Самая большая рамка представляет множество всех цепочек составленных из алфавита TNT. Следующая вложенная в нее рамка - множество всех правильно построенных цепочек TNT. В пределах этого пространства и находится множество всех высказываний TNT. Теперь начинается самое интересное. Множество теорем изображено как крона дерева, растущая из ствола (представляющего набор аксиом). Дерево как символ было выбрано из-за сходства процесса роста с рекурсией, которым возникают новые теоремы: новые ветви (теоремы), постоянно вырастают их старых. Отпочковывающиеся ростки дерева проникают во все уголки ограниченного рамкой пространства, формируя тем самым множество истин, но не могут заполнить пространство полностью. Граница между множеством истин и множеством ложных утверждений, как предполагается, представляет собой бесконечно ветвящийся фрактал, который, независимо от того, как глубоко вы исследуете его, всегда имеет более тонкие уровни ветвления и излома, следовательно, границу невозможно точно определить любым конечным способом (См. книгу Манделброта "Фракталы".) Зеркальное дерево представляет множество отрицательных теорем. Все они ложные, но его ветви все же неспособны охватить все ложные высказывания. Они не охватывают все пространство ложных утверждений. [Рисунок автора.]

Фигура и фон в музыке

Можно так же найти фигуру и фон в музыке. Один пример - различие между мелодией и сопровождением. К мелодии всегда приковано наше внимания, а сопровождение в некотором смысле ей только помогает. Поэтому мы удивлены, когда находим на заднем плане партии основную мелодию. Это редко бывает в поп-музыке. Обычно о сопровождении не думают как о переднем плане. Но в музыке барокко, особенно в музыке Баха, часто различные линии исполнения либо выступают вперед, либо отступают назад, подобно фигуре и фону постоянно меняются местами. В этом смысли партитуры Баха можно назвать "рекурсивными".
Другая аналогия дихотомии фигура-фон в музыке - это разделение музыке на главную тональность и синкопу. Если вы будете считаете тона как "основной, пол-тона, треть-тона, четверь-тона" то обычно ноты соответствуют порядку тональностей. Но иногда мелодия бывает преднамеренно сдвинута на одну тональность, чтобы явно ее выделить. Это происходит, например, в некоторых этюдах для фортепиано Шопена. Такой же прием широко используется Бахом. Особенно в его сонатах для несопровождаемой скрипки, а также в партии для несопровождаемой виолончели. Здесь Бах ухитряется получить две или более линии звучания, идущие одновременно. Иногда он (это при наличии только солирующего инструмента) использует так сказать "двойные аккорды" - две ноты непосредственно. Однако, в других случаях он вставляет один голос в мелодию, а другой в сопровождение так, что мы слышим их как две различные мелодии, переплетающиеся и гармонирующие друг с другом. Само собой разумеется, Бах не останавливается на этом уровне сложности. . . *

* К сожалению, "перевод" этого раздела - почти полнейшая галиматья. Если вы разбираетесь в музыкальной теории, то сразу это поймете. Если нет, то вам может показаться, что здесь скрыт смысл, который просто недоступен. Но это- иллюзия. Смысл оригинального текста для меня тоже остался неясен. Поэтому я соединил слова без особого беспокойства о содержании. Главное - чтобы красиво звучало. Если вы попались на эту уловку, то, возможно, утешитесь следующим наблюдением. Получилось, что обычно "солирующий" смысл почти исчез, но хорошо прорисованный "фон" убедил вас в существовании некой глубокомысленной "фигуры" Подобые иллюзии не редко встречаются в жизни. Особенно - в политике. . . Прим А. С.

Рекурсивно-счетные множества и рекурсивные множества

Теперь позвольте понятие фигуры и фона перенести обратно в область формальных систем. В нашем примере роль позитивного пространства сыграли теоремы C-типа, а роль отрицательного пространства сыграли цепочки с простым числом дефисов. Пока единственный путь, который мы нашли, чтобы представить простые числа типографским способом - представить их как негативное пространство. Но имеется ли( не зависимо от того насколько это сложно) способ представить простые числа как позитивное пространство? То есть можно ли найти все простые числа, как множество теорем некоторой формальной системы?

У разных людей разная интуиция и они подсказывает им различные ответы. Я очень ярко помню, как был удивлен и озадачен после того, как понял разницу между позитивным и негативным описанием. Я был весьма убежден, что не только простые числа, но и любое множество чисел, которое можно представлены как негатив, всегда можно представить и как позитив. Интуиция, лежащая в основе моей веры выражается вопросом: "Как могут фигура и фон не нести одну и ту же информацию?" Они, казалось мне, воплощают ту же самую информацию, только закодированную двумя дополняющими друг друга способами. Вы с этим согласны?

Оказывается, я был прав по поводу простых чисел, но был не прав вообще. Это удивило меня и продолжает удивлять даже сегодня. Но факт, что:

Существуют формальные системы, чье отрицательно пространств (множество не-теорем) не является позитивным пространством (множеством теорем) какой-либо формальной системы.

Этот результат, оказывается, имеет ту же глубину, что и Теорема Геделя. Поэтому не удивительно, что моя интуиция здесь не сработала. Я, так же как и математики начала XX века, ожидал от мир формальных систем и натуральные числа большей предсказуемости. Говоря техническим языком, получается:

Существуют рекурсивно-счетные множества, которые не рекурсивны.

Словосочетание рекурсивно-счетный (часть сокращаемое до "r.e.") - математический близнец нашему понятию "курсивно прорисованный", а понятие рекурсивный - близнец "рекурсивно прорисованный". Для некоторого множества цепочек, быть "r.e", означает, что оно может быть получено согласно типографским правилам. Таково, например, множество теорем C-типа и множество теорем MIU-системы. В действительности рекурсивно-счетным будет множество теорем любой формальной системы. Это можно представить по аналогии идеей "фигуры" как "множество линий, которые можно построить по законам изобразительного искусства" (и не важно, что эти линии могут означать!). Рекурсивное же множество подобно той фигуре, чей фон - тоже фигура. То есть рекурсивное множество не только "r.e." но и его дополнение тоже "r.e." *

* Здесь наша интуиция играет с нами злую шутку. Представьте себе троглика, который варкливо-чуватый. Теперь представьте троглика чуватого. Является ли всякий вакрвиво-чуватый троглик одновременно и чуватым? Естественно думать, что оба троглика варклиы но один из них еще и чуватый. То есть варкливо-чуватые трогличи есть разновидность варкливых трогликов вообще. Но вы ошиблись так же как, с рекурсивно-счетными и "просто" рекурсивными множествами. Все наоборот! Варкливо-чуватый не обязательно варкливый. Варкливые есть разновидность( подмножество) варкливо-чуватых! Почему? У трогликов так принято. И весь тут сказ! Прим. А. С.

Из вышеупомянутого результата следует:

Существуют формальные системы, для которых не существует никакой разрешающей процедуры реализуемой типографским способом.

Из чего это следует? Очень просто. Типографская разрешающая процедура - это метод, который отличает теоремы от не-теорем. Существование такого теста позволяет нам последовательно производить все не-теоремы. Для этого, двигаясь по списку всех цепочек, вы каждую испытываете разрешающей процедурой. По результату вы отбраковываете плохо формализованные цепочки и теоремы, оставляя одни не-теоремы. Описанная процедура соответствует типографскому методу получения множества не-теорем. Но согласно более раннему утверждению (которое мы здесь приняли на веру), для некоторых систем это невозможно. Поэтому, признав его, мы вынуждены заключить, что и типографские разрешающие процедуры существуют не для всех формальных систем.

Предположим, что мы нашли множество натуральных чисел F, ('F'- анг. "фигуры"), которое мы можем произвести некоторым формальным способом, на подобии множества составных чисел. Предположим, что его дополнение - множество G ('G'- англ. "основание", фон), на подобии простых чисел. Вместе множества F и G составляют множество натуральных чисел. Мы знаем правило, по которому мы можем получить все числа множества F. Но мы не знаем никакого подобного правила для получения всех чисел множества G. Важно понять, что если члены множества F всегда производятся в порядке увеличения размера, то мы всегда можем выделить и G как негатив. Но проблема в том, что многие "r.e." множества перечисляются методами, которые выдают свои элементы в произвольном порядке. Поэтому вы никогда не знаете, будет ли число, которое вы только что перескочили, получено когда-нибудь в будущем или нет, если вы подождите процесс какое-то время еще.*

* точно выяснить это можно только за бесконечный промежуток времени, но такая ситуация нам уже неприятно знакома. Прим. А. С.

Мы ответили "нет" на вопрос: "являются и все фигуры рекурсивными?" Мы теперь видим, что аналогично должны ответить и на подобный вопрос в математике: "Являются ли все множества рекурсивными?" С этой точки зрения давайте теперь вернуться к неуловимому термину "форма". Позвольте взять наше множество-форму F и множество-фору G. Мы можем согласиться что все числа в множестве F имеют некоторую общую "форму". Но можно ли тоже сказать относительно чисел множества G? Это странный вопрос. Когда мы имеем дело с бесконечными множествами, например с натуральными числами, то "дыры" созданные удалением некоторого подмножества, очень трудно определить некоторым явным способом. И может случиться так, что они не связаны друг с другом никаким общим признаком или "формой" вообще. В последнем случае вопрос вкуса хотите ли вы для такого понятия использовать термин "форма" или нет, но размышлять о нем как о некой форме - провокация. Быть может лучше не определять "форму" твердо, а оставить ее пластичной.*

* Давайте определим форму как контур, который смело можно закрасить некоторым цветом. Позитивные элементы однозначно имеют форму. По мере их обнаружения (перечисления) мы "обводим" их контуром и смело закрашиваем белым цветом. Но как поступать с негатиом?! Если мы знаем, что больше никогда не вернемся туда, где только что покрасили ВСЕ белые формы, то можно смело закрашивать черным и промежутки между ними. Негатив тоже приобретает форму (именно приобретает, процесс бесконечен, но в любой момент мы имеем "затвердевшую" часть формы, не подлежащую переделке). А если уверенности нет? Если в промежутке есть пока еще неизвестный позитив? А мы его закрасим черным?!. . . Значит, к закраске черных промежутков (получению негативной формы) мы сможем приступить только, когда определим ВСЕ белые формы. То есть спустя бесконечность. . . Прим. А.С,

Имеется головоломка, для размышления над вышеизложенными вопросами. Вы можете характеризовать следующую последовательность чисел (или их отрицательное пространство)?

1 3 7 12 18 26 35 45 56 69 . . .

Чем эта последовательность напоминает фигурно-фигурную фигуру?

Простые числа: проступают как фигура, а не фон

В конце концов, что с формальной системой для простых чисел? Как ее построить? Наша уловка должна обойти умножение и прямо перескочить к неделимости, как позитивно представленной сущности. Имеются схема аксиом и правило вывода для создания теорем, которые выражают представление, что одно число не делит ('DND' - 'does not divide') другое число.

Схема аксиом: xyDNDx, где х и у - разные цепочки дефисов (X не равно Y).

Например _ _ _ _ _ DND _ _ где x заменен на '_ _' , а у на ' _ _ _ '

Правило:

DND

Если вы используете это правило дважды к приведенной выше аксиоме, то получите такую теорему: _ _ _ _ _ DND _ _ _ _ _ _ _ _ _ _ _ _

Которая интерпретируется, как "5 не делит 12". Но _ _ _ DND _ _ _ _ _ _ не теорема. Что происходит не так, как надо, если вы попробуете получить ее?

Теперь чтобы определить, что данное число является простым, мы должны получить некоторое знание относительно его свойства неделимости. В частности мы хотим знать, что некоторое число не делимо ни на 2, ни на 3, ни на 4 и т. д. все до числа меньшего на 1 чем оно само. Но мы не можем быть столь неопределенны в формальных системах, чтобы говорить "и так далее". Мы должны разъяснить это. Мы хотели бы иметь способ высказать на языке системы "число Z свободно от делителей не больших X". что означает: никакое число от 2 до Х не делит Z. Это может быть сделано, но нужна уловка. Подумайте об этом, если хотите. Вот это решение:

Правило

DND

Правило

DND

Эти два правила охватывают понятие неделимости. Все что мы теперь должны делать, это сказать, что простое число это такое, которые неделимы на число, меньшие на 1 чем оно само:

Правило

_DF

Да! не стоит забывать что 2 - простое число!

Аксиома

P_ _

И так мы получили все что хотели. Формальное представление простых чисел. Иметься испытание на неделимость, которое может быть сделано без какого-либо отслеживания назад. Вы можете уверенно двигаться вверх, проверяя сначала неделимость на 2, затем на 3 и так далее. Это "монотонный" или "однонаправленный" процесс. Здесь нет необходимости во взаимной игре удлинение-сокращение. Нам нет нужды в попеременном увеличении и уменьшении длинны цепочек для того, чтобы выследить все простые числа. Но у формальных систем есть и такая возможность. И именно эта потенциальная возможность формальных систем непредсказуемо перемешивать предыдущее с последующим, в итоге влечет такие ограничивающие результаты как Теорема Геделя, Проблема Остановки Тьюринга и тот факт, что не все рекурсивно-счетные множества рекурсивны.